- Selecting Treatments
- Replication
- Randomization
- Plot Size
- Experimental Designs
- Data Collection
- Collecting Unbiased Data
- Statistical Calculations
- Summary
As farmers and farm advisers, you make many management choices during a growing season. For example, you may have to decide which cultivar to plant, which herbicide to use, how frequently to apply a fungicide, and what rate of nematicide to use. Often the information needed to make the best decision is available to you, but when it is not available you can frequently compare the options by conducting your own small experiments. Your experiments can be just as valid as any university study if you follow a few important principles of experimental design.
All experiments have certain things in common, so designing an experiment usually includes the following steps. You must decide what question you want to have answered. This is the goal, or objective, of the experiment. The goal of the experiment will dictate what to include in the experiment to help you answer your question. The individual things that you wish to test in your experiment are called "treatments" and the physical areas to which the treatments are applied are called "plots." Then you need to decide how the treatments should be physically arranged in the field. Technically, this is what is called the "experimental design."
Experiments answer your original question by allowing you to make unbiased comparisons among the treatments you selected. You will need some way to evaluate how well each treatment worked to make comparisons among treatments. The information you collect to help you make those comparisons (such as yield, insect counts, or disease severity) is called "data." Finally, you need an objective way to evaluate the data. This is usually done through statistical analysis.
Selecting Treatments
The objective, or purpose, of the study will determine the treatments included in an experiment. Writing down the test objectives is helpful because this forces you to define them precisely. A test may have more than one objective, although multiple objectives should be closely related.
The selection of treatments is usually logical if you can define the purpose of the study; all treatments necessary to address the test's objective should be included. For example, if the purpose were to determine which of five fungicides works the best, then the treatments would include all five of those fungicides. If the purpose were to determine if any of the five fungicides works better than your current choice, then the treatments would include the five fungicides plus the fungicide you currently use. Accurately stating the purpose of the test before the treatments are applied in the field is critical. After the treatments have begun, it will be too late to add other treatments to answer the question you really wanted to address.
The selection of treatments and the experimental design get more complicated as the question you are trying to answer gets more complex. It is common to want to test in the same experiment two (or more) things that influence crop production. For example, you may want to test chicken litter as a fertilizer and test five corn hybrids to maximize yield. The specific questions addressed in this case are:
- What effect does chicken litter have on corn production?
- What effect do the hybrids have on corn production?
- Does chicken litter have the same effect on each hybrid?
The third question may not be as obvious as the first two, but it will always be asked or implied if you are testing two or more factors in the same experiment. In this example, you have to determine what the effect of chicken litter is on each hybrid and then compare those effects to each other. To do that, the treatment list must include each hybrid without chicken litter and each hybrid with chicken litter (a total of 10 treatments). With this list of treatments, you can make the comparisons necessary to answer our three questions. This example employs a "factorial arrangement of treatments" that will be discussed in more detail in a later section.
One final note about treatment selection involves including additional treatments to provide a relative measure of effect. Comparing the yield of five new corn hybrids does little good if you cannot tell how those yields compare with the hybrids you already grow. You should include at least one hybrid with which you are already familiar (often called a "standard" treatment) to provide a relative measure of how well the new hybrids produce. If you wish to test a new nematicide, you should include a treatment with the currently used nematicide and a treatment with no nematicide as a basis for comparison. Such treatments are known as "checks" or "controls." Without the proper controls, you will not be able to say that the new nematicide worked better than the currently used nematicide or even that the new nematicide worked better than no nematicide! The questions you wish the experiment to answer should indicate what treatments should be included as controls.
It is frequently desirable to have both a positive and a negative control in an experiment. The negative control helps you determine if the treatments being tested work better than some minimal treatment (or nothing) and positive controls help you determine if the treatments being tested work better than the current standard practice. You may have several control treatments in an experiment if you currently have several viable options from which to choose. For example, if you currently can choose either of two fungicides to control a leafspot problem, you may wish to include them both as controls in your experiment when you test new products. You do not have to include all currently available options as controls for the experiment to be useful, but you can.
Replication
In an experiment, replication means that individual treatments (such as each of the five pesticides being tested in an experiment) have been applied to more than one plot. Replication is necessary because all test plots are not identical, and that leads to variation in the data you collect; you will not get exactly the same results from two plots that received the same treatment. You can take steps to minimize the effect of variation if it has an identifiable cause, but there will always be some variation among plots that cannot be controlled. In statistical terms, uncontrolled variation is called experimental error. The purpose of replication is to allow you to make a more accurate estimate of how each treatment performed even though there is uncontrolled variation in the experiment. This can best be shown in an example.
Suppose you have 10 rose bushes and you want to test if a new fungicide will protect the bushes from black spot, a fungal leaf disease. You could pick five plants to leave untreated as a control and spray the other five with the fungicide. Later, when black spot is evident on the leaves, you count the number of diseased spots on each plant and compare the two treatments. The five untreated plants have 26, 21, 19, 25, and 23 infected spots (a treatment mean, or average, of 22.8 spots per plant), and the fungicide treated plants have 20, 15, 18, 21, and 20 spots (a mean of 18.8). Statistical analysis indicates that the fungicide did in fact reduce the number of infected sites, but you would not be able to determine that if you only had one treated and one untreated plot. Think about the following examples based on the data above. If you only had two plants and the untreated plant had 26 spots and the treated plant had 15 spots, it may seem easy to determine that the fungicide reduced disease. But what if the untreated plant had 19 spots and the treated plant had 21 spots? You might conclude that the fungicide did not work or even that it increased disease! Adequate replication can minimize this problem.
It is common when you have several replications of each treatment to have data like that in the rose example above: The treatment means are different but individual measurements may overlap. In this example, the lowest measurement from the untreated plants was 19, and the highest measurement from the fungicide treated plants was 21, but the treatment means were 22.8 for the untreated plants and 18.8 for the treated plants. Replication of treatments increases your ability to detect differences in treatment means. Having more replications allows you to identify (statistically) smaller differences in treatment means than you could identify with fewer replications.
The number of replications that you need is influenced by the biology of what you are testing, how close together the treatment means are, and how much variation exists within a treatment. For field tests in plant pathology, nematology, weed science, soil fertility studies, and entomology, a minimum of four replications is suggested, but five or six replications are much better. If treatment means are close together or variation is relatively large among the plots that received the same treatment, then you may need more replications to detect differences among treatments.
Just as the data may vary within a replicated treatment, the results may vary among experiments if the whole experiment is repeated. This can happen because of different weather conditions, different disease or insect pressure, or many other factors beyond your control. This does not mean that the results of a single experiment are not valid, but it does make it dangerous to draw conclusions from a single experiment. The one set of results you have may indicate treatment differences, but if you repeated the test several times you might not see those treatment differences again. If the test is repeated (and that means you cannot change any of the treatments) and you get similar results, then you can be much more confident that your conclusions are correct.
Randomization
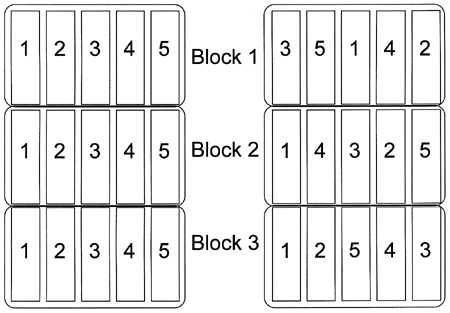Figure 1. Test plots on the left are not randomized. Plots on the right are randomized. The numbers (1-5) represent the five treatments in this test.Randomization in an experiment means that the treatments are assigned to plots with no discernable pattern to the assignments. The reason randomization is important is that the positioning of treatments within the block may affect their performance. One example of this is an experiment testing five corn hybrids (labeled 1 through 5) in which you plant the hybrids in the same order in each block: 1, 2, 3, 4, then 5 (see figure 1). If hybrid 2 is naturally much taller than the others, it can slightly shade the hybrids planted next to it (hybrids 1 and 3) and unfairly make them look a little bit worse than they would look if they were not planted next to hybrid 2. Another example is a field in which soil fertility gets progressively lower as you cross the field from east to west so that productivity is reduced as you go from one side of the field to the other. If two corn hybrids are planted side by side but within a block, hybrid 1 is always planted on the east side of hybrid 2, then hybrid 1 is always planted in slightly more fertile soil and therefore has an unfair advantage.
In both of the preceding examples, randomization could have prevented the unintentional bias because the arrangement of the treatments would have been different within each block. Because you cannot anticipate all the influences that may introduce bias into a test, ALL experiments should be randomized. There are many ways to randomize treatments within a block, but the simplest is literally to pull the numbers out of a hat. Assign each treatment a number, write the numbers on individual pieces of paper, mix the slips of paper up, and then select the slips one at a time without looking at them first. The order in which the numbers are drawn is the order in which they will be arranged in a block. Repeat these steps for each block in the experiment.
If you wish to use the experiment as a demonstration plot (such as for a field day), it is common that one block not be truly randomized. This is done so that particular treatments can be seen side-by-side to facilitate comparisons and highlight differences for casual observers. Though it is better to randomize all blocks and not intentionally arrange treatments, arranging the treatments in one block is unlikely to affect the test's results as long as the other blocks are truly randomized.
Plot Size
A plot, the area to which an individual treatment is applied, can be any size, including a single plant growing in a pot or 5 acres or more of a field. Before you can apply treatments to your test area, you must decide how large your plots should be. Although there is a lot of subjectivity in selecting plot size, there are some important considerations including the equipment to be used in planting, harvesting, and treatment application; how much space is available for use in the experiment and how many other treatments there are; and the biology of what you are studying. Accommodating equipment and space concerns makes it easier to conduct the test. Accommodating biological concerns reduces the chances of overlooking differences among treatments. Equipment and space considerations are usually easy to identify, but biological considerations are not always obvious.
If you have equipment to plant, harvest, and apply treatments to four rows at a time, then the logical plot width would be some multiple of four rows (four rows, eight rows, 12 rows, etc.). Any other width (such as six rows) would make it more difficult to conduct the experiment. The length that plots should be is more flexible than plot width. For example, if you plan to weigh the harvest from each plot, the scales you have may influence the length plots should be. If you have scales that are designed for weighing hundreds of pounds, your plots should be large enough to provide a harvest weight that can be accurately determined by your equipment, and increasing the length of plots is an easy way to do that. Also, the length of your plots may be adjusted so that all of your plots (all replications of all treatments) will fit into the area available for your test. If you have a large area for your test, space may not be an important consideration.
To accommodate biological considerations, you should answer two questions:
- How large a plot is needed to observe the biological effect (disease severity, insect damage, weed frequency, nematode population levels, etc.) that you are studying?
- How large a plot is needed to minimize the influence of a treatment (chemical application, etc.) on the plots next to it?
By answering these questions, you can determine the minimum plot size necessary to get useful data from the experiment.
To get an accurate measurement of the effect of pest management treatments, the plot must be large enough to account for uneven initial distribution of the pest (pathogen, insect, weed, etc.). Some areas may start with the pest present, but the pest may occur in other areas only after it has spread from its initial location. This is very important for pests that spread very slowly (such as most soilborne organisms).
Some diseases and pests are highly mobile and spread very rapidly (such as many insects). In an insect management trial, measuring the effect of a treatment can be very difficult if your plots are too small because the insects that you see in the plot may have simply spread from the plot next to it. To minimize this problem, you can increase your plot size and then collect data from the middle section of the plot. For example, you might have an eight-row plot but only collect data from the middle four rows. The rows from which you do not collect data are often referred to as "buffer rows" because they buffer the effect of the neighboring plots. If you do not use buffer rows when they are needed, you may fail to detect differences among treatments and incorrectly conclude that many treatments were ineffective. Buffer rows are frequently used when there is uncertainty whether treatments can influence nearby rows.
A similar concept involves the use of border rows along the edges of your test area. A significant "border effect" commonly exists at the edge of a field where the plants may grow differently than plants not at the edge. Although you may be able to minimize this problem with blocking, it is often better to eliminate the problem by not using the rows at the edge of a field in your experiment.
Once the plots are large enough to be representative of a much larger area, further increasing plot size will not significantly improve the accuracy of the results. For example, in an experiment testing fungicides for control of white mold, or stem rot, in peanut, a four-row-wide by 100-foot-long plot should be just as good as an eight-row-wide by 400-foot-long plot. Plots that are larger than necessary take more field space and may increase the amount of work required for an experiment, but they usually will not adversely affect the test results unless the plots get so large that the plots within a block are no longer uniform. Plots that are too small may prevent the accurate assessment of treatment effects. If the space available for an experiment is limiting, having more replications is usually more beneficial than having larger plots as long as your plot size allows accurate assessment of treatment effects.
Experimental Designs
Completely Randomized Design
The completely randomized design is the simplest experimental design. In this design, treatments are replicated but not blocked, which means that the treatments are assigned to plots in a completely random manner (as in the left side of figure 2). This design is appropriate if the entire test area is homogeneous (uniform in every way that can influence the results). Unfortunately, it is rare that you can ever be confident of a test site's uniformity, so a completely randomized design is rarely used in field tests. The completely randomized design is used more commonly in greenhouse tests, though blocking is often useful even in the more controlled environment of a greenhouse.
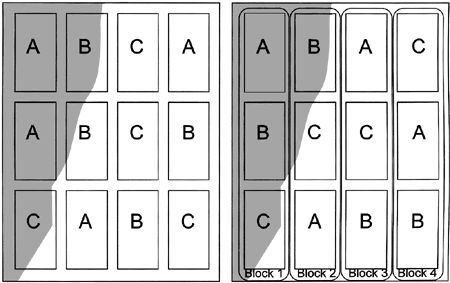Figure 2. The shaded area represents an area of the field that is different from the unshaded area. Treatments (A, B, and C) are replicated but not blocked in the field on the left. On the right, treatments are replicated and blocked; each block contains one plot of each treatment.Randomized Complete Block Design
The randomized complete block design is the most commonly used design in agricultural field research. In this design, treatments are both replicated and blocked, which means that plots are arranged into blocks and then treatments are assigned to plots within a block in a random manner (as in the right side of figure 2). This design is most effective if you can identify the patterns of non-uniformity in a field such as changing soil types, drainage patterns, fertility gradients, direction of insect migration into a field, etc. If you cannot identify the potential sources of variation, you should still use this design for field research but make your blocks as square as possible. This usually will keep plots within a block as uniform as possible even if you cannot predict the variation among plots.
Blocking refers to physically grouping treatments together in an experiment to minimize unexplained variation in the data you collect (referred to as experimental error). This allows the statistical analysis to identify treatment differences that would otherwise be obscured by too much unexplained variation in the experiment. Variation in an experiment can be divided into two types: variation for which you can account in the statistical analysis and variation that is unexplained. The goal in blocking is to allow you to measure the variation among blocks and then remove that variation from the statistical comparison of treatment means. If you can anticipate causes of variation, you can block the treatments to minimize variation within each block and remove some variation from the statistical analysis. The mathematics of how blocking allows you to reduce unexplained variation is beyond the scope of this bulletin.
In the most common experimental designs, a block will contain one plot of each treatment in the experiment. If an experiment has five treatments, then each block will contain five plots, with each plot receiving a different treatment. When a block contains one plot of each treatment, then each block represents one replication of each treatment. For this reason, blocks are frequently referred to as "replications" or "reps," but the concept of blocking should not be confused with the concept of replication; replication and blocking serve different purposes. In agricultural research, field plots are almost always blocked even when no obvious differences are present in the field. It is much better to block when you did not really need to than not to block when you should have blocked.
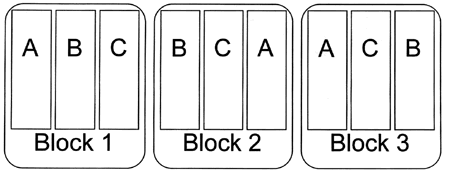Figure 3. An easy way to arrange blocks is to put them side by side across the field. Letters represent different treatments.Blocking is a very powerful tool that is most effective if you can anticipate sources of variation before you begin an experiment. For example, in a herbicide trial, one side of a field may have a history of more severe weed problems. If you just scattered your treatments randomly through the field, a lot of the variation in the data you collected could be due to the increased weed pressure on one side of the field. Such variation would make it difficult to determine how well each treatment worked. Because you know one side of the field will have more weeds, you can remove that source of variation from the statistical analysis by blocking and improve your chances of identifying differences among treatments.
The process of blocking follows a logical sequence. First, you determine that there is something (weeds, drainage, sun/shadow, water, soil type, etc.) that is not uniform throughout the experimental area (field, greenhouse, etc.) that may influence whatever you are measuring (yield, plant height, etc.). Then you can arrange your treatments into blocks so that the area within each block is as uniform as possible (see figure 2). Though the area within a block should be relatively uniform, there may be large differences among the blocks, but that is what makes blocking effective. Your goal is to maximize the differences among blocks while minimizing the differences within a block.
The shape of the blocks is not important as long as the plots within a block are as uniform as possible. Ideally, the only differences among plots within a block should be due to the treatments. Blocks in field experiments are usually square or rectangular, but they may be any shape. Blocks in the same experiment do not have to be the same shape; the shape of individual blocks will be determined by variation in the field that you are trying to minimize. If you are not sure what shape your blocks should be, square or nearly square blocks are usually a safe choice.
Blocks may be arranged through the field in many ways. If the field is wide enough, an easy way to arrange blocks is to place them side-by-side all the way down the field (see figure 3). But blocks do not have to be contiguous and may be scattered through the field in any way that is convenient for you.
Factorial Arrangement of Treatments
A factorial arrangement of treatments is not an experimental design, though you will often hear it referred to as a factorial design or a factorial experiment. A factorial arrangement of treatments means that the experiment is testing two or more factors at the same time, and that the experiment includes all combinations of all factors. The term "factor" is used to describe a group of treatments that have something in common. Fungicides, sources of nitrogen, or corn hybrids could be considered factors in an experiment. Factors may be defined broadly or narrowly in different experiments. All herbicides may be grouped as a factor in one experiment, but pre-plant and post-plant herbicides may be treated as separate factors in another experiment. A single-factor experiment tests one factor at a time; a two-factor experiment tests two factors at once.
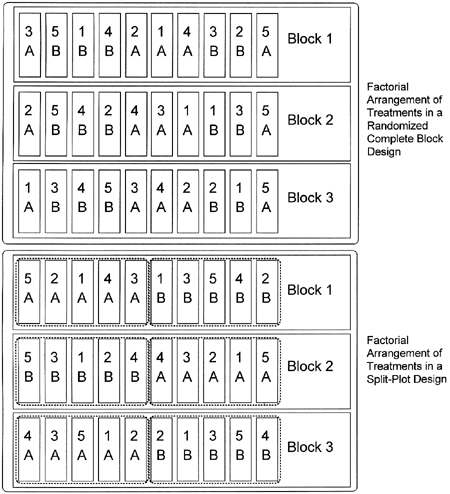Figure 4. A 2x5 factorial arrangement of treatments in a randomized complete block design (above) and in a split-plot design (below). A and B represent two levels of one factor, and the numbers (1-5) represent five levels of a second factor. The combinations (e.g., 4A, 5B, etc.) denote individual treatment combinations. Either experimental design could be used, but the randomized complete block design is preferred unless the split-plot design is required by some limitation on randomization.
Most simple on-farm experiments are single-factor experiments (in a Completely Randomized or Randomized Complete Block design) and compare things such as crop varieties or herbicides, but it is sometimes useful to test two or more factors at once. For example, a two-factor experiment would allow you to compare the yields five corn hybrids at three planting dates. This accomplishes three things at once:
- It allows you to compare the corn hybrids with each other.
- It allows you to evaluate the effect of planting date.
- It allows you to determine if varying the planting date changes the relative performance of the hybrids (e.g. one hybrid may only perform well if planted early).
The first two could be done in separate single-factor experiments, but the third can only be achieved by having both factors in a single experiment. This becomes especially important if one factor can have a significant influence on the effect of the other factor. For example, you might test soybean varieties as one factor and nematicides as another factor. If a few varieties have good nematode resistance but others do not, they may appear equally good when effective nematicides are used but varieties with resistance would appear much better when nematicides are not used. In cases like this, the effect of one factor (variety) is strongly influenced by the other factor (nematicide). When one factor influences the effect of the other factor, there is said to be a significant interaction between the two factors. It can be very important to know if there is an interaction between factors, because if there is an interaction, you can make predictions or recommendations based on the results of single-factor experiments ONLY when all other factors are at the same levels they were at in the experiment. If you change some factor not included in the experiment, the results from your single-factor experiment may no longer be valid.
With a factorial arrangement of treatments, all values (or levels) of each factor must be paired with all levels of the other factors. If you have two nematicides and five soybean varieties, then your treatment list must include each variety with each nematicide for a total of 10 treatments. This would be referred to as a "two by five factorial" to denote how many factors were present in the experiment and how many levels of each factor were used. The number of treatments increases quickly when you add more levels for a factor (if you used three nematicides instead of two, you would have 15 treatments instead of 10), so choose your levels carefully or the experiment can get too large to manage.
A factorial arrangement of treatments can be a very powerful tool, but because the number of treatments can get very large it is best used when some reason exists to believe that the factors may influence each other and have a significant interaction. If there is no suspicion that the factors may influence each other, it is frequently easier and more thorough to test the factors in separate experiments. A factorial arrangement of treatments can be used with a completely randomized experimental design or a randomized complete block design. The top half of figure 4 shows a factorial arrangement of treatments in a randomized complete block design.
Split-Plot Experimental Design
A split-plot experimental design is a special design that is sometimes used with factorial arrangements of treatments. This design usually is used when an experiment has at least two factors and some constraint prevents you from randomizing the treatments into a randomized complete block design. Such a constraint may be based on equipment limitations or on biological considerations. For example, the equipment you have may make it difficult to put out a soil fumigant in randomized complete blocks, but you may be able to put out the fumigant so that all treatments within a block that get the fumigant will be clustered together rather than scattered throughout the block. You can use a split-plot experimental design to work around this limitation as long as you are able to randomize the other factors. There are other situations when this design is appropriate, but a constraint on randomization is the most likely to occur.
Suppose you want to test the effect of five fungicides to control Cylindrocladium Black Rot on two varieties of peanut. In this test, you would have a 2x5 factorial arrangement of treatments: The two factors would be varieties (2 levels of this factor) and fungicides (5 levels of this factor). Because a factorial arrangement of treatments is not an experimental design, you still have to select an experimental design that best meets your needs. If you are able to randomize varieties and fungicides within a block, then you should pick a randomized complete block design. If there is some reason why you cannot completely randomize the treatments within each block, then you may be able to use a split-plot design to work around that limitation. For example, you may have a six-row planter but only enough space in the field to put out four-row plots. To resolve this dilemma, you could plant all of the plots that have the same peanut variety together within a block and then randomize the five fungicide treatments within each peanut variety.
In split-plot designs, the terms "whole plots" and "sub-plots" refer to the plots into which the factors are randomized. As the names imply, whole plots are subdivided into subplots. In figure 4, a whole plot would be the areas designated with A or B, and the subplots, the subdivisions within the whole plots, are designated 1, 2, 3, 4, or 5. In this example, A and B could represent two varieties (two levels of one factor) and the numbers could represent different fungicides (five levels of a second factor). Each whole plot serves as a block for the subplot treatments.
To assign treatments in a split-plot design, start by identifying where each block will be. Then randomize the whole plot treatments within each block. The whole plot treatments will be the treatment that you are unable to randomize into a randomized complete block design. The subplot treatments can then be randomized within each whole plot treatment (see figure 4).
Data Collection
You can collect an almost infinite amount of data in any experiment, but not all of it will be useful. Proper planning will ensure that you collect the right data to address your test's objective. The "right" data to collect can usually be determined by examining the stated purposes of the experiment. For example, if the objective of a peanut leafspot fungicide trial is "to evaluate the ability of five fungicides to reduce leafspot incidence and severity," then collecting data on leafspot incidence and severity and peanut yield should seem obvious. Collecting data on rainfall and temperature, which strongly influence leafspots on peanut, may be worthwhile because it can help you explain your results. But collecting data on soil physical properties does not seem to be related to the objective. It is useful to ask yourself, "How can this data be used?" If you have trouble answering that question, then collecting that data may be a waste of time. It is much more common for people to collect too little data than to collect too much data.
Deciding what data to collect is only part of the process. You also have to decide when to collect that data and if you need to collect the same type of data on more than one occasion. For example, in a nematicide trial, it is not sufficient to collect nematode population data at harvest; you must also collect data at planting to ensure that the plots started out equal. It is usually a good idea to collect nematode population data in the middle of the season because even in effective treatments nematode populations can sometimes increase to the level of the untreated control by the end of the season. The biology of the organisms involved will determine when and how frequently data should be collected.
So, how much data is enough? The answer is "enough data to fully address the test's objective." If you understand the biology of the organisms involved and how your data addresses the test objective, then you should be able to tell if you are collecting enough data.
You should take photographs of any differences among treatments that are easily visible. To most farmers, a picture is more convincing than a graph or data table.
Collecting Unbiased Data
It is critically important to collect unbiased data. The only way to ensure this is to collect data without knowing what the treatment was in that plot. That would be difficult to do if the treatment were written on a stake in front of each plot. It is beneficial to use some type of code on the plot stakes so that you have to decode the stake number to determine what the treatment was. You can make up any code you like just so long as the person collecting the data cannot tell from the plot stake what the treatment was. For example, you can number the plots sequentially (1, 2, 3, etc.) and have a sheet of paper listing what treatment was applied to plot 1, plot 2, etc. When you collect the data, you write down your observation for plot 1 and later look at your list to see what treatment was in that plot.
If you know what treatment was in a plot, or which plots were the untreated controls, your evaluations (disease severity ratings, insect damage ratings, etc.) may inadvertently be influenced. Your subconscious may slightly increase the ratings for untreated plots and decrease it for the plots with treatments that you think should work well. You will probably not even be aware that it is happening, but these subtle influences can change the data enough to affect your ultimate conclusions from the test. If you do not collect unbiased data, you cannot be certain that your conclusions are correct.
Statistical Calculations
After collecting data from a properly designed experiment, you will usually need to analyze the data with appropriate statistical calculations. Statistical analysis may not be necessary if treatment differences are very large and consistent; treatment means may then be sufficient. Statistical analysis is beyond the scope of this publication. Proper statistical analysis can be done if your experiment was designed according to the principles outlined in this publication, but proper analysis can be complicated greatly if these principles were not followed.
It is probably best for you to seek help in making statistical calculations. If your experiment was properly designed, Extension specialists and other scientists may be willing to help you with the statistics if you involve them early in the process. They can also check your proposed design for flaws and omissions. If you want to do the work yourself some simple statistics can be calculated by hand, but most people will make the calculations with the help of computer software. Specialized statistical software is available, but most spreadsheet software can calculate simple statistics.
Summary
The following checklist can be used in designing an experiment. These items may be addressed in any order.
- Determine the objective of the test.
- Select treatments to address the objective. Consider including positive and negative controls.
- Determine what data should be collected, and when it should be collected, to address the objective.
- Select the number of replications to use. Consider four replications a minimum.
- Determine how big individual plots will be.
- Select an experimental design.
- Determine how blocks should be arranged in the field.
- Randomize treatments within blocks.
Properly designing and implementing a field trial may seem complex the first time, but it is really a logical process that should not be intimidating. You may need help the first time you design a trial to ensure that you are not overlooking something important, but if you learn the principles involved in the process, you should quickly gain confidence in your ability to conduct experiments on your own.
Status and Revision History
Published on May 01, 1999
Published on Feb 09, 2009
Published on Apr 28, 2009
Published with Full Review on Apr 25, 2012
Published with Full Review on Jan 30, 2017